The FLoWeRS metric starts with the assumption of homogeneity and isotropy of space. It also assumes that the spatial component of the metric can be time-dependent. The generic metric which meets these conditions is
 ranges over a 3-dimensional space of uniform curvature, that is, elliptical space, Euclidean space, or hyperbolic space. It is normally written as a function of three spatial coordinates, but there are several conventions for doing so, detailed below.
ranges over a 3-dimensional space of uniform curvature, that is, elliptical space, Euclidean space, or hyperbolic space. It is normally written as a function of three spatial coordinates, but there are several conventions for doing so, detailed below. 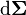 does not depend on t — all of the time dependence is in the function a(t), known as the "scale factor".
does not depend on t — all of the time dependence is in the function a(t), known as the "scale factor".
Aucun commentaire:
Enregistrer un commentaire